Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son:
Origen
O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene.
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.


Magnitudes Escalares
Propiedades
Conmutativa: a+b=b+a
Asociativa: (a+b)+c=a+(b+c)
Elemento Neutro: a+0=a
Elemento Simétrico: a+(-a)=a-a=0
Vectores unitarios
Cualquier vector puede ser considerado como resultado de la suma de tres vectores, cada uno de ellos en la dirección de uno de los ejes coordenados.

Producto escalar de dos vectores
El producto escalar de dos vectores, expresado analíticamente como r · v, se obtiene de la suma de los productos formados por las componentes de uno y otro vector. Es decir, dados dos vectores r y v, expresados en un mismo sistema de coordenadas:
r = rxi + ryj + rzk
v = vxi + vyj + vzk
v = vxi + vyj + vzk
el resultado de multiplicar escalarmente r por v es:
r · v = rx· vx + ry · vy+ rz · vz
Planos en el espacio
Recta
Operando en la ecuación vectorial de la recta llegamos a la igualdad:
Esta igualdad se verifica si:
Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:
Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.

Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Un plano queda determinado por un punto P y un par de vectores con distinta dirección.
Para que el punto P pertenezca al plano π el vector
Plano
Ecuaciones paramétricas del plano
Operando en la ecuación vectorial del plano llegamos a la igualdad:
Esta igualdad se verifica si:

Ecuación general o implícita del plano
Un punto está en el plano π si tiene solución el sistema:

Este sistema tiene que ser compatible determinado en las incógnitas λ y µ· Por tanto el determinante de la matriz ampliada del sistema con la columna de los términos independientes tiene que ser igual a cero.

Sustituimos:
Realizamos las operaciones y le damos a D el valor:
Obtenemos la ecuación general de plano:
Ecuación canónica o segmentaria del plano
Sean los puntos A(a, 0, 0), B(0, b, 0) y C(0, 0, c), la ecuación



Semana 2
Limites y Continuidad
Una función vectorial es una aplicación  tal que a cada vector
tal que a cada vector  le hace corresponder
le hace corresponder  Denotamos
Denotamos
donde  que denominamos componentes o proyecciones de
que denominamos componentes o proyecciones de  , con lo cual
, con lo cual  .
.
Ejemplo 5.14.: sea  esta función sería un ejemplo de una función vectorial, a cada vector de
esta función sería un ejemplo de una función vectorial, a cada vector de  le hace corresponder un vector de
le hace corresponder un vector de  , y las componentes son:
, y las componentes son:
Definición 5.18.: sea  . Sea
. Sea  un punto de acumulación de
un punto de acumulación de  y sea
y sea  . Se dice que
. Se dice que  si
si
Observación 5.6.: análogamente a los casos anteriores se verifica, el teorema de unicidad de límites. Sin embargo no se puede hablar de producto, cociente y potencias en  , por tanto, los resultados del algebra de límites sólo se verifican para la suma.
, por tanto, los resultados del algebra de límites sólo se verifican para la suma.
Proposición 5.3.: Sea  con
con 
 y sea
y sea  , son equivalentes
, son equivalentes
Proposición 5.4.: Sea  con
con 
 ,
,  es continua en
es continua en  es continua en
es continua en  .
.
Observación 5.7.: Por lo tanto estudiar los límites y continuidad de una función vectorial no es más difícil que estudiar los límites y continuidad de una función escalar, solamente será más largo, puesto que será suficiente con estudiar las  funciones escalares componentes.
funciones escalares componentes.
Semana 3
Derivada
Funciones vectoriales.
En este resumen, escribiremos todo en el espacio euclidiano tridimensional R3
.
Una función vectorial es una función que transforma un numero real en un vector:
donde x(t), y(t) y z(t) son funciones reales de variable real.
Así, se dice que F es continua, derivable o integrable, si lo son x(t), y(t) y z(t).; y ademas su derivada y su
integral se calculan del siguiente modo:
.
Algunas reglas de derivaci´on de estas funciones relacionadas con las operaciones entre vectores son las siguientes
(suponemos que F y G son dos funciones vectoriales, u es una funci´on real de variable real y λ ∈ R):
Se ve f´acilmente, que todas son “heredadas” de las reglas de derivaci´on de las funciones reales de variable real.
Lo mismo ocurre con las integrales:
Semana 4





Semana 5
Triedro Móvil
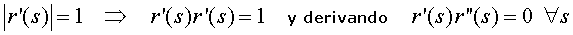
En cada punto de la curva C donde r''(s)≠0 están definidos los tres vectores siguientes
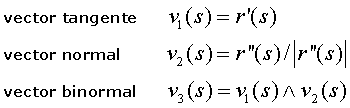
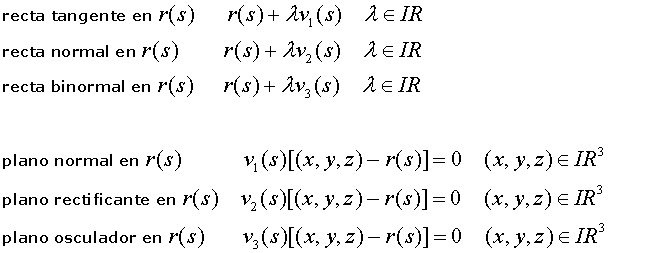
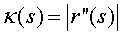
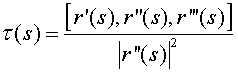
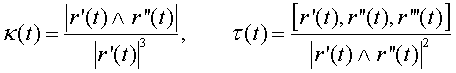
En este resumen, escribiremos todo en el espacio euclidiano tridimensional R3
.
Una función vectorial es una función que transforma un numero real en un vector:
donde x(t), y(t) y z(t) son funciones reales de variable real.
Así, se dice que F es continua, derivable o integrable, si lo son x(t), y(t) y z(t).; y ademas su derivada y su
integral se calculan del siguiente modo:
.
Algunas reglas de derivaci´on de estas funciones relacionadas con las operaciones entre vectores son las siguientes
(suponemos que F y G son dos funciones vectoriales, u es una funci´on real de variable real y λ ∈ R):
Se ve f´acilmente, que todas son “heredadas” de las reglas de derivaci´on de las funciones reales de variable real.
Lo mismo ocurre con las integrales:
Semana 4
Vector Tangente y Normal
La tangente de una curva es una recta que intersecta la curva en un solo punto. Es conocido por nosotros a través del cálculo que mediante la diferenciación de una función se obtiene el punto tangencial para la curva de esa función. Un concepto similar es aplicable al cálculo vectorial, junto con una excepción.
Para una función con un vector de la forma, (x), un vector de la forma es llamado vector tangente en el caso de que esta función sea real y su magnitud no sea igual a cero. En esta situación, la tangente de la función dada (x) en un punto arbitrario es paralela al vector tangente, en ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito esencial. Esto es debido a que un vector de magnitud cero no puede tener dirección.
De manera similar, un vector tangencial unitario es definido como,



Aquí s es la longitud total del arco dado, (t) es el vector posición de la función dada y t es la variable de parametrización.

En la figura anterior, X es un punto estático, mientras que P es un punto en movimiento. El punto P se mueve lentamente en la dirección del punto X, mientras el punto P se acerca al punto X, el vector desde el punto X hasta el punto P se acerca al vector tangente en el punto X. La recta que contiene el vector tangente se conoce como recta tangencial.
Un vector normal es algo similar a un vector unitario, suponga que para una función (x), (t) es el vector posición, entonces el vector normal para la función dada es definida como,

En cada punto de una curva, el plano osculador es el plano que contiene a su vector tangente y al vector normal a la curva. Para una partícula desplazándose en el espacio tridimiensional, el plano osculador coincide con el plano que en cada instante contiene a la aceleración y la velocidad. La ecuación de este plano viene dada por:
Donde:
 , el punto de la trayectoria.
, el punto de la trayectoria. , el vector velocidad en el punto considerado.
, el vector velocidad en el punto considerado. , las coordenadas de un punto genérico del plano osculador.
, las coordenadas de un punto genérico del plano osculador.
Si se tiene una partícula en la posición  , moviéndose con velocidad
, moviéndose con velocidad  y sometida a una aceleración
y sometida a una aceleración  el plano osculador viene dado por el conjunto de puntos:
el plano osculador viene dado por el conjunto de puntos:
 , moviéndose con velocidad
, moviéndose con velocidad  y sometida a una aceleración
y sometida a una aceleración  el plano osculador viene dado por el conjunto de puntos:
el plano osculador viene dado por el conjunto de puntos:
Obviamente si la partícula tiene un movimiento rectilíneo el plano osculador no está definido.
Semana 5
Triedro Móvil
Sea r=r(s) con s Є I una parametrización natural de una curva C de clase C3. Como s es un parámetro longitud de arco se tiene
En cada punto de la curva C donde r''(s)≠0 están definidos los tres vectores siguientes
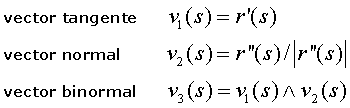
El sistema de vectores anterior es ortonormal y se denomina triedro móvil de Frenet. Asociados a cada uno de los vectores del triedro móvil tenemos una recta y un plano:
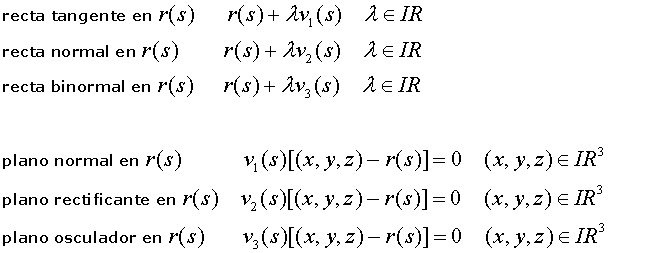
El triedro móvil se encuentra definido sólo en aquellos puntos en los que r''(s)≠0. Si este vector es nulo en un conjunto discreto de puntos de la curva, entonces la curva queda dividida por estos puntos en arcos en los que sí se tendrá triedro móvil. Las curvas para las que r''(s)≠0 en un intervalo serán, en dicho intervalo, un segmento de recta.
Definición Se denomina curvatura de una curva C en un punto r(s) siendo s un parámetro longitud de arco a
Intuitivamente la curvatura mide lo que se le falta a la curva para ser una recta en cada punto.
Definición Se denomina torsión de una curva C en un punto r(s) siendo s un parámetro longitud de arco a
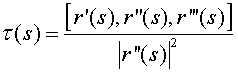
Intuitivamente, la torsión mide lo que le falta a la curva para estar contenida en un plano, es decir, para ser una curva plana.
Para un parámetro arbitrario t se tiene
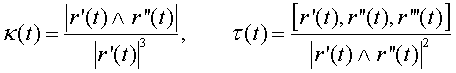
Teorema Es condición necesaria y suficiente para que una curva sea una recta que la curvatura sea idénticamente nula.
Teorema Es condición necesaria y suficiente para que una curva no rectilínea sea plana que la torsión sea idénticamente nula.





No hay comentarios:
Publicar un comentario